📌 문제 설명
방향 그래프가 주어졌을 때,
1번 정점에서 N번 정점으로 가는 모든 경로의 개수를 구하는 프로그램을 작성한다.
예를 들어 아래 그래프에서 1 → 5로 가는 경로는 총 6가지다.
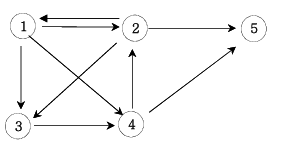
1 → 2 → 5
1 → 3 → 4 → 2 → 5
1 → 3 → 4 → 5
1 → 4 → 2 → 5
1 → 4 → 5
1 → 2 → 3 → 4 → 5📝 입력 & 출력
입력
- 첫 줄에 정점의 수 N(1 ≤ N ≤ 20), 간선의 수 M이 주어진다.
- 다음 M줄에 걸쳐 방향 간선 정보 A B가 주어진다. (A → B)
출력
- 1번 정점에서 N번 정점으로 갈 수 있는 모든 경로의 가지 수를 출력한다.
🔹 예제 입력 & 출력
예제 입력
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
예제 출력
6💡 해결 방법
- 방향 그래프를 인접리스트(ArrayList) 로 표현
- DFS를 통해 1번 정점에서 N번 정점까지의 모든 경로를 탐색
- 방문 여부는 ch[] 배열을 통해 관리
- 한 경로 탐색이 끝나면 백트래킹을 통해 방문 상태 복구
💻 코드 구현 (Java)
전체 코드
package partRecursiveTreeGraph;
import java.util.*;
public class Problem12 {
static int n, m, answer = 0;
static ArrayList<ArrayList<Integer>> graph;
static int[] ch;
public void DFS(int v) {
if (v == n) answer++;
else {
for (int nv : graph.get(v)) {
if (ch[nv] == 0) {
ch[nv] = 1;
DFS(nv);
ch[nv] = 0;
}
}
}
}
public static void main(String[] args) {
Problem12 T = new Problem12();
Scanner kb = new Scanner(System.in);
n = kb.nextInt();
m = kb.nextInt();
graph = new ArrayList<>();
for (int i = 0; i <= n; i++) graph.add(new ArrayList<>());
ch = new int[n+1];
for (int i = 0; i < m; i++) {
int a = kb.nextInt();
int b = kb.nextInt();
graph.get(a).add(b);
}
ch[1] = 1;
T.DFS(1);
System.out.print(answer);
kb.close();
}
}📖 코드 설명
1️⃣ 그래프 초기화 및 인접리스트 생성
graph = new ArrayList<>();
for (int i = 0; i <= n; i++) graph.add(new ArrayList<>());- 각 정점마다 연결된 정점들을 리스트로 관리
- 인덱스 1부터 사용하므로 0~N까지 생성
2️⃣ 간선 정보 입력
int a = kb.nextInt();
int b = kb.nextInt();
graph.get(a).add(b);- a → b 방향 간선 추가
- 방향 그래프이므로 단방향만 저장
3️⃣ 방문 체크 및 DFS 호출
ch[1] = 1;
T.DFS(1);- 시작 정점은 항상 1번
- 방문 체크한 후 DFS 시작
4️⃣ DFS 함수: 경로 탐색
public void DFS(int v) {
if (v == n) answer++;
else {
for (int nv : graph.get(v)) {
if (ch[nv] == 0) {
ch[nv] = 1;
DFS(nv);
ch[nv] = 0;
}
}
}
}- 현재 노드가 목적지 N이라면 answer++
- 아니면 현재 노드에서 갈 수 있는 다음 노드들을 모두 확인
- 아직 방문하지 않았다면 방문 표시 후 DFS → 이후 백트래킹
⏳ 시간 복잡도 분석
- 가능한 모든 경로를 DFS로 탐색하므로
- 시간 복잡도는 O(총 경로 수 × 평균 경로 길이)
- 그래프 구조에 따라 지수적으로 늘어날 수 있음
- N ≤ 20이므로 완전 탐색으로도 무리가 없다.
🧠 핵심 정리
- 인접리스트는 간선 수가 많을 때 인접행렬보다 메모리 효율이 좋다.
- DFS로 모든 경로를 탐색하고, 방문 배열과 백트래킹을 통해 중복 방지
- 방향 그래프에서는 단방향 연결만 추가하는 것을 주의해야 한다.
출처: 인프런 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비
https://www.inflearn.com/course/자바-알고리즘-문제풀이-코테대비/dashboard
자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비 강의 | 김태원 - 인프런
김태원 | , 자바(Java) 알고리즘 문제풀이 채점사이트를 통해 기초부터 준비해보세요! 💪 [사진] 이 강의는 [사진] 자바(Java)로 코딩테스트 준비를 하고 계신 분께 추천드려요! 문제는 기초~ 중급
www.inflearn.com
'코딩테스트 > 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비' 카테고리의 다른 글
| 섹션 8 DFS, BFS - 1. 합이 같은 부분집합(DFS : 아마존 인터뷰) (0) | 2025.05.02 |
|---|---|
| 섹션 7 Recursive, Tree, Graph - 14. 그래프최단거리(BFS) (0) | 2025.05.02 |
| 섹션 7 Recursive, Tree, Graph - 11. 경로탐색 (인접행렬) (0) | 2025.04.30 |
| 섹션 7 Recursive, Tree, Graph - 10. Tree 말단 노드까지의 가장 짧은 경로 (0) | 2025.04.30 |
| 섹션 7 Recursive, Tree, Graph - 8. 송아지 찾기(BFS : 상태트리탐색) (0) | 2025.04.29 |

